Python Global Interpreter Lock (GIL) + numerical data processing

The global interpreter lock may naively seem to imply that a Python process can only use one core of a processor. That is not at all the case: one (well-known) reason is that Python extension code (such as ubiquitous NumPy/SciPy kernels) can themselves use multiple threads. This is what I'd call fine-grained threading, which is easy to use and effective when the kernels have available sufficient parallelism. Coarse-grained parallelism through the threading module can however also be effective for the following reasons.

The Python GIL ensures that the Python interpreter in a process is only ever executing one opcode (Python instruction) at any one time. Instructions in a compiled extension to Python, or a syscall do not intrinsically need to the lock acquired, and indeed the lock is released before most such calls, e.g., the lock is released before NumPy kernels are called. For this reason many different NumPy kernels from /different Python threads/ can be executing at the same time, utilising multiple CPU cores.

Illustration

As an illustration I've slightly Adapted the code Travis posted here (http://technicaldiscovery.blogspot.co.uk/2011/06/speeding-up-python-numpy-cython-and.html) so that it uses either threading or multiprocessing for coarse-grained threading. The multiprocessing approach uses multiple Python processes and so can not be affected by the GIL.

# Adapted from: http://technicaldiscovery.blogspot.co.uk/2011/06/speeding-up-python-numpy-cython-and.html
from numpy import zeros, array_split, linspace

import threading
import multiprocessing

NT=1

dx = 0.1
dy = 0.1
dx2 = dx*dx
dy2 = dy*dy


def num_update(u):
    u[1:-1,1:-1] = ((u[2:,1:-1]+u[:-2,1:-1])*dy2 +
                    (u[1:-1,2:] + u[1:-1,:-2])*dx2) / (2*(dx2+dy2))

def py_update(u):
    nx, ny = u.shape
    for i in range(1,nx-1):
        for j in range(1, ny-1):
            u[i,j] = ((u[i+1, j] + u[i-1, j]) * dy2 +
                      (u[i, j+1] + u[i, j-1]) * dx2) / (2*(dx2+dy2))

def calc(N, Niter=100, func=py_update, icl=[1]):
    for ic in icl:
        u = zeros([N, N])
        u[0] = ic
        for i in range(Niter):
            func(u)


def blot(np=100, N=30, mp=False, num=True):
    threads=[]
    if num:
        update=num_update
    else:
        update=py_update
    for icl in array_split(linspace(1,2,np), NT):
        if mp:
            t=multiprocessing.Process(target=calc, args=(N, 30, update, icl,))
        else:
            t=threading.Thread(target=calc, args=(N, 30, update, icl,))
        t.start()
        threads.append(t)
    for t in threads:
        t.join()

Measuring the performance of this example as function of number of threads (NT) gives following results:

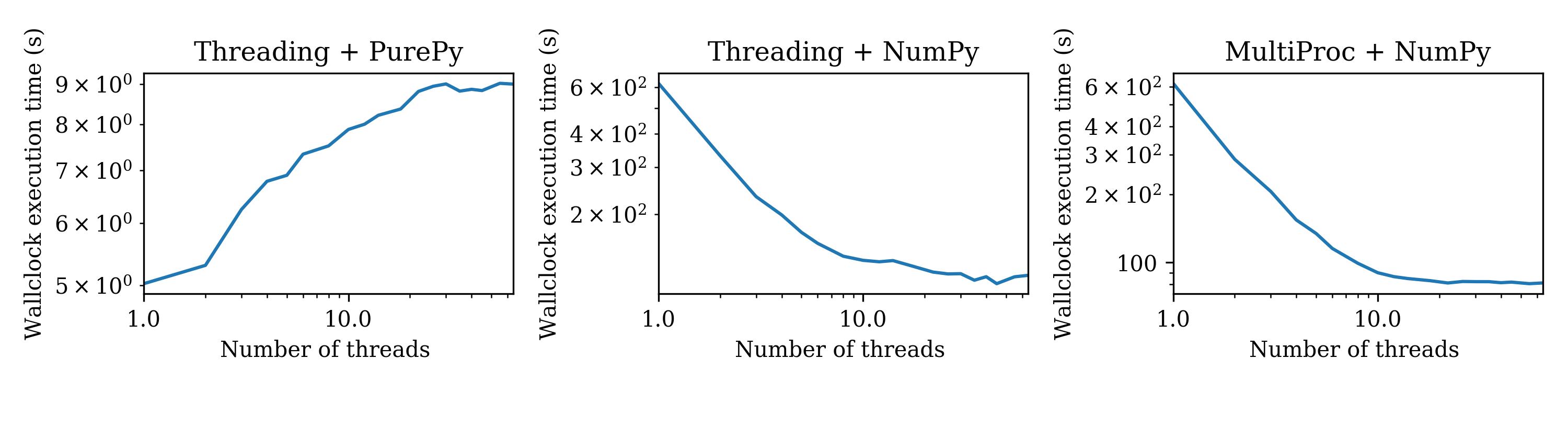
The graph labelled Threading+PurePy is for the pure Python version of the problem. It can be seen there is a small increase in the execution time as more threads are added. This is due to the GIL: each pure Python thread has to acquire the lock in order to execute any instructions, so speed of execution engine can never be faster than single threaded. The small increases in execution time are due to overheads of acquiring the GIL and switching between the threads.

The graph labelled Threading+NumPy uses NumPy kernels for the computation. It can be seen that as the number of threads increases execution time decreases close to linearly and then levels off. A similar pattern can be seen in the MultiProc+Numpy, in which the multipricessing module is used instead of threading. In both of these scenarious the speed of execution with multiple threads exceeds the single core case, demonstrating that GIL is not limiting the execution to an equivalent of one core. It can be seen that multiprocessing performance levels of at slightly faster than threading but it isn't clear if this is due to lock-acquisition and thread switching overheads or due O/S level effects.