Using QuantLib to generate a Brownian Bridge

This is a very short article illustrating how to use the QuantLib library Brownian bridge code. The reason there can be some confusion is that the code takes a sequence of random variates as input for the bridge construction code. The first variate in this sequence is taken to represent the global step of the bridge, i.e., how much the value of the underlying changes over the entire period (for bridge of length of unit time only). If the first variate is set to zero, then the standard Brownian bridge that begins and ends at zero will be created.

The code

Here is a simple program that uses the QuantLib library to generate a Brownian bridge:

/**
   Copyright (C) 2009 Bojan Nikolic <bojan@bnikolic.co.uk>

   Output a realisation of a Brownian Bridge from QuantLib

*/

#include <iostream>

#include <time.h>
#include <boost/random/normal_distribution.hpp>
#include <boost/random/mersenne_twister.hpp>
#include <boost/random/variate_generator.hpp>


#include <ql/quantlib.hpp>

/// Prints the bridge, including the cumulative sum of the variations
/// which is the actual path of the underlying
void printBridge(const std::vector<double> &b)
{
  double cumsum=0;
  for(size_t i=0; i<b.size(); ++i)
  {
    cumsum+=b[i];
    std::cout<<i+1
          <<","
          <<b[i]
          <<","
          <<cumsum
          <<std::endl;
  }
}


void bbridgeout(void)
{
  const size_t n=500;

  QuantLib::BrownianBridge bridge(n);

  std::vector<double> inp(n);

  // This is the key fact: the first variate in the input sequency is
  // used to construct a global step. If you want the usual Brownian
  // bridge, you need to set this to zero.
  inp[0]=0.0;

  // Generate the rest of the variates as standard Gaussian random
  // values
  boost::variate_generator<boost::mt19937, boost::normal_distribution<> >
    generator(boost::mt19937(time(0)),
           boost::normal_distribution<>());

  for(size_t i=1; i<inp.size(); ++i)
    inp[i]=generator();

  std::vector<double> out(n);
  bridge.transform(inp.begin(),
                inp.end(),
                out.begin());

  printBridge(out);
}

int main(void)
{
  bbridgeout();
  return 0;
}

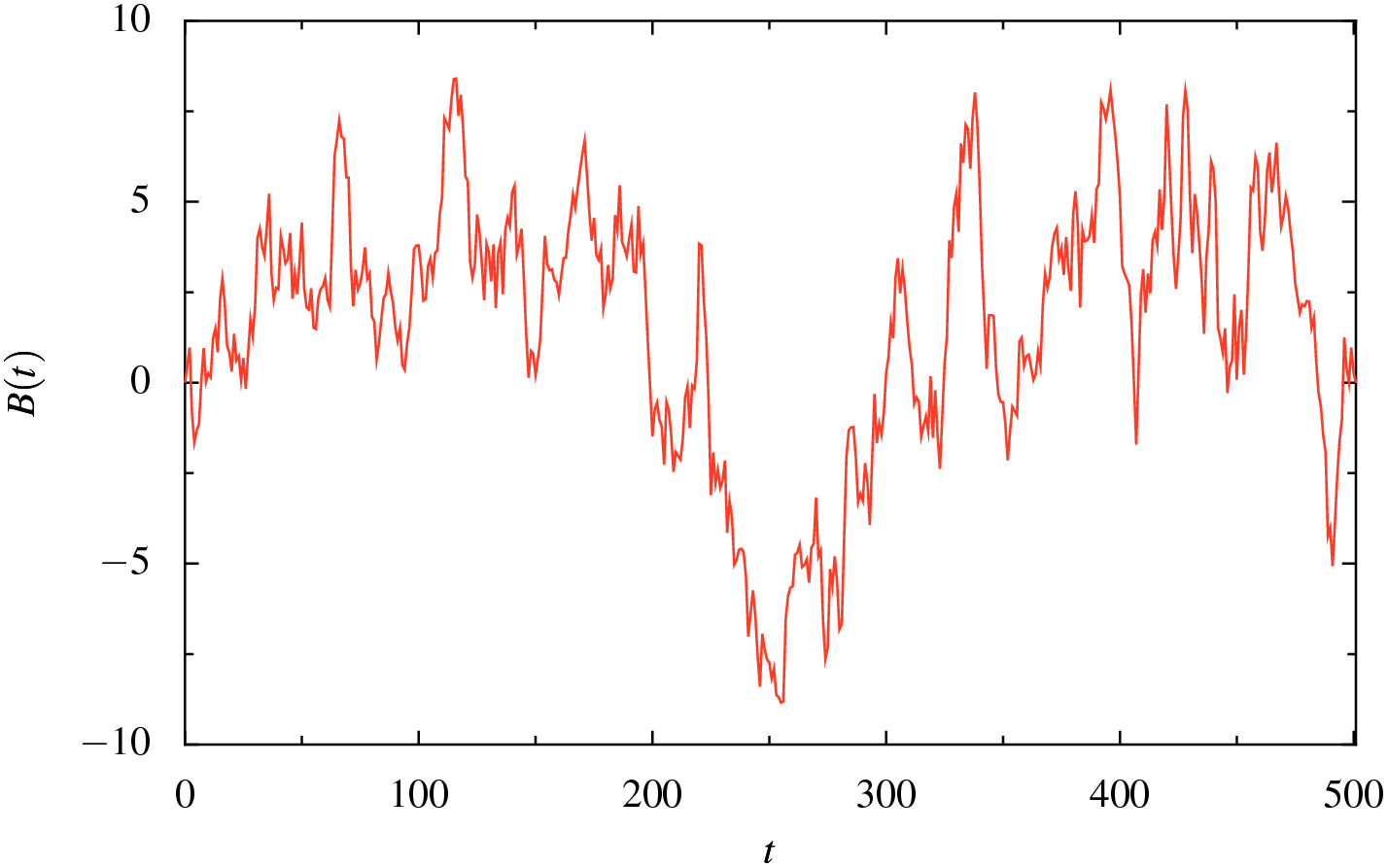
A sample realisation

Here a sample path produced by the Brownian bridge program:

A sample realisation of the Brownian bridge processes