Calculating the present value of CDS contracts¶
The model¶
The contingent leg¶
The underlying integral which models the price of the contingent part of the CDS contract is:
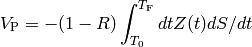
where:
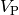 is the value at the present time of the contingent
leg of the CDS contract
is the value at the present time of the contingent
leg of the CDS contract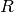 is the recovery fraction
is the recovery fraction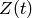 is the discount function, as defined by the zero curve
is the discount function, as defined by the zero curve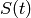 is the survival probability
is the survival probability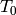 is the time at beginning of risk
is the time at beginning of risk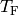 is the time at end of risk
is the time at end of risk
The value of the above integral is evaluated using the approximation that the combination of the spread and zero curves are piecewise flat. In that approximation, the integral is evaluated exactly in the usual way using the sum:
![V_{\rm P}=(1-R)\sum_i \frac{\lambda_i}{\lambda_{i}+f_{i}}
\left[1 - \exp\left(-\Delta t_i(\lambda_i+f_i)\right) \right] s_{i} d_i](_images/math/b5b957720170809bfa8c0becc1b7e0232987928e.png)
where
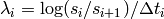
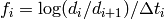
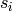 is discount factor at time
is discount factor at time 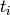 computed from the
spread curve
computed from the
spread curve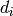 is the discount factor at time
is the discount factor at time 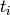 computed from
the zero curve
computed from
the zero curve 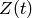
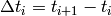
The set of time points, 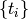 used in this sum are the
union of:
used in this sum are the
union of:
- All dates appearing in the zero (or discount) curve
- All dates appearing in the spread curve
The fee leg¶
There are two conventions for determining if the fee leg should be payable in case of a default of the reference names and the choice of these naturally affect the valuation of the present value. The two possibilities are:
- The fixed rate coupon is only paid if there is no default by the day the full coupon amount has accrued (the accrual end date is not necessarily the same as the payment date)
- Or, the coupon is paid in full if there is no default by the end-of-accrual date and the fractional amount of the coupon accrued by the default date is paid if a default does occur
The fee leg of contract adopting the first (no accrual payment on default) convention is valued very simply as discounted value of the coupon payment times the survival probability:
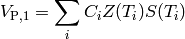
where as before 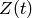 is the discount function and
is the discount function and 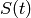 is the survival probability, and
is the survival probability, and 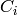 is the amount of the
is the amount of the
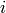 -th coupon payment.
-th coupon payment.
In the case of the second convention noted above (i.e., if a default
occurs before the end of the accrual of the coupon, the fractional
accrued amount is paid), the value 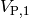 needs to be
increased by the expected value of the fractional accrued
amount. Therefore the value of the coupon payments when the contract
are made with the second convention can be written as:
needs to be
increased by the expected value of the fractional accrued
amount. Therefore the value of the coupon payments when the contract
are made with the second convention can be written as:
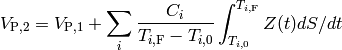
The integral within the sum over coupon payments can be evaluated in a way similar to the integral for the contingent leg, leading to an exact result in the case that the rates are flat-forward.