Lazy Code Generation (LzCG) and C++ Expression Templates

The idea here is simple: to interrogate the hardware at load-time or run-time and select one of several pre-prepared algorithms already available as object code. These algorithms would have been created to be optimal for some representative systems. This is presumably the approach taken by some of the well-known commercial numerical libraries.

The advantages of such an approach are that:

• A simple, standard, application binary interface (ABI) can be presented to the application which is easily usable from all languages including C, C++ and FORTRAN
• Only object code needs to be distributed

There are however a number of disadvantages:

• Only a certain, small, number of functions (or expressions) can be supported by the library in this way since all of these need to be bundled together with the library
• Only a finite number of alternative algorithms for each function can be shipped while there is a very wide variety of hardware combinations. Therefore the algorithm selected may not be optimal for the particular hardware combination being run

By stochastic selection I mean that a number of alternative algorithms for each function to be supported are benchmarked on the target computer and the algorithm with best performance in this benchmark is selected. Because only the object code for the best algorithm needs to be retained, and because the results of previous tests can be used as a guide of which algorithms it is worth trying, a much larger space of algorithms can be explored, leading to potentially better performance. However, for this to be done at build time, the build of the library needs to be made on the target machine.

The advantages of this approach are:

• The standard simple ABI is presented to the application
• The algorithms are tuned for the precise machine on which they are run

The disadvantages are:

• Only a small, pre-defined, number of functions can be supported by the library
• Installation of the library involves a build stage making it potentially more complex

Here the algorithm selection happens at run time, from a set of pre-prepared object code templates. These templates can represent different families of algorithms and each can have some adjustable parameters which can be iterated over during algorithm selection.

The advantage of this approach is that:

• The algorithm can be tuned on parameters of the functions, e.g., the dimension of a transform operation or the size of a matrix

This is the most complex and powerful approach: The expression to be executed is passed (in some sort of code) to a compiler at run-time, and the compiler can then use information about the available hardware to generate code for the expression that has been passed, and then subsequently this run-time generated code is run.

The advantages of this approach are:

• The number of functions or expressions that can be optimised is unlimited as they are interpreted and code for them is generated at run-time
• Precise tuning for the hardware used can be employed

The disadvantages of this approach are:

• It can be hard to integrate correctly with a compiled language like C++

Obviously when the computer has a number of cores or when an graphics/auxiliary processing unit is present then large improvements in performance can be achieved by correctly using these resources to the maximum. C-like languages like OpenCL and CUDA are an attempt to provide a programming paradigm that is closer aligned to practicalities of programming of numerical algorithms on many core-systems.

We now look at the process by which the C++ compiler translates the above function to object code. In broad terms, what a numerical expression template library is concerned with is line 8 of the example above. In particular, the code can be made more efficient by:

• Avoiding generation of a temporary variable
• Carrying out the addition and assignment in a single loop through the code

A useful of understanding this process is to turn off all the optimisations and look at the assembly code generated by the compiler. If we look at the code for the function above that we are using our example, the key line is:

call _ZN5boost7numeric5ublas6vectorIdNS1_15unbounded_arrayIdSaIdEEEEaSINS1_13vector_binaryIS6_S6_NS1_11scalar_plusIddEEEEEERS6_RKNS1_17vector_expressionIT_EE

if we turn the function signature back into standard C++ type syntax, we get an even longer output:

call boost::numeric::ublas::vector<double, boost::numeric::ublas::unbounded_array<double, std::allocator<double> > >& boost::numeric::ublas::vector<double, boost::numeric::ublas::unbounded_array<double, std::allocator<double> > >::operator=<boost::numeric::ublas::vector_binary<boost::numeric::ublas::vector<double, boost::numeric::ublas::unbounded_array<double, std::allocator<double> > >, boost::numeric::ublas::vector<double, boost::numeric::ublas::unbounded_array<double, std::allocator<double> > >, boost::numeric::ublas::scalar_plus<double, double> > >(boost::numeric::ublas::vector_expression<boost::numeric::ublas::vector_binary<boost::numeric::ublas::vector<double, boost::numeric::ublas::unbounded_array<double, std::allocator<double> > >, boost::numeric::ublas::vector<double, boost::numeric::ublas::unbounded_array<double, std::allocator<double> > >, boost::numeric::ublas::scalar_plus<double, double> > > const&)

This function signature is so long in part because it encodes in one signature both of the operations in line 8 of our example function; i.e., it combines the assignment and addition operations. We can decipher the meaning of the signature as follows:

• First look at the name of the function by looking for the identifier before the "(" token – this is operator=
• As this is a member function, next look for the class that it is the member of – in this case this is ublas::vector<>
• Next look for the return type, which in this case is also ublas::vector<> in this case
• Next look for the template parameters of the function itself – in this case it is ublas::vector_binary<>
• Finally look for the types of the parameters to the function – in this case there is one parameter of type ublas::vector_expression<>

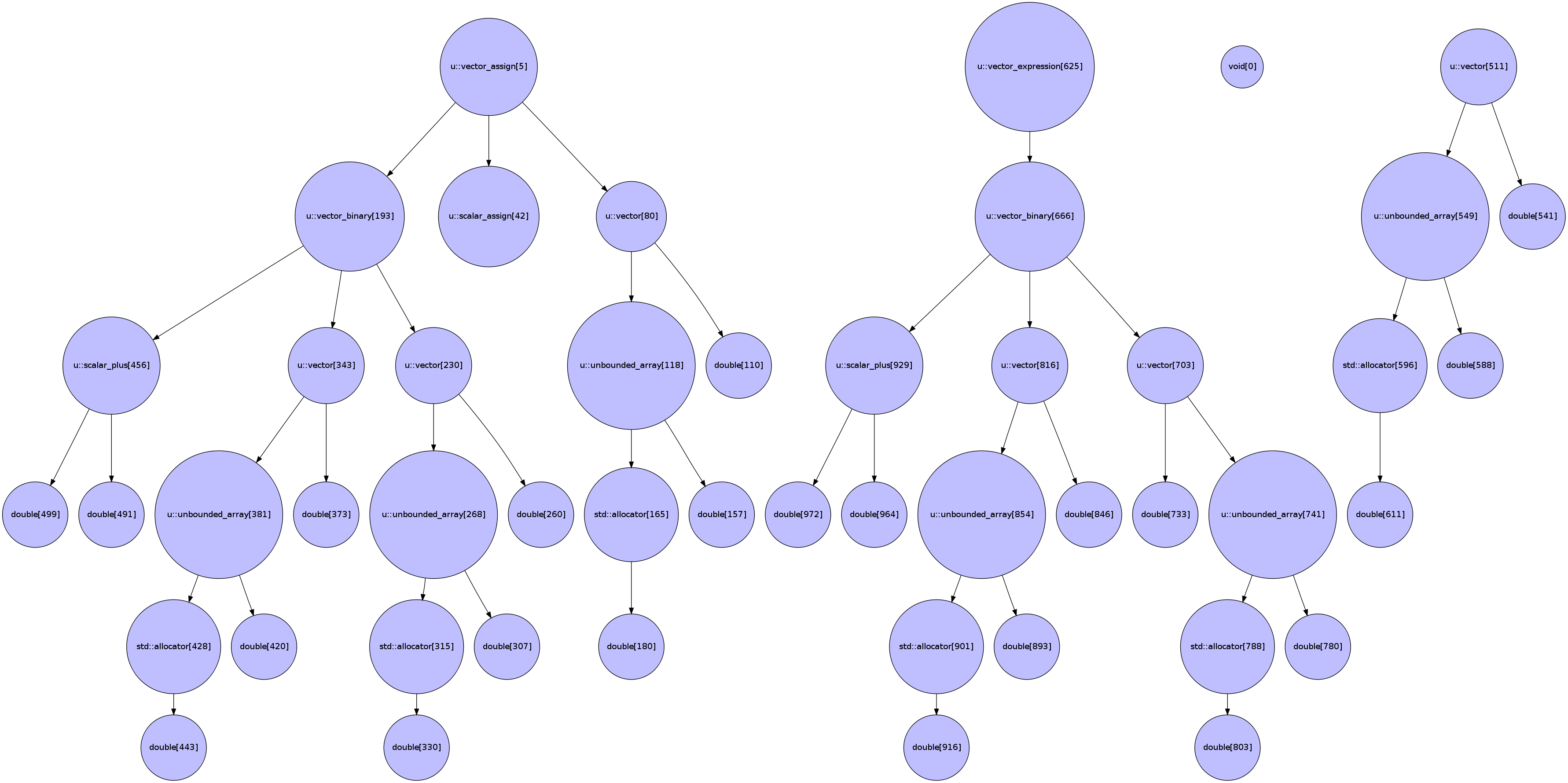
So in broad terms, the function being called is an assignment operator for a ublas::vector<> which assigns directly from a (binary) vector expression. To understand the function signature in detail we need to look at the parameters to the templates. Even for a relatively simple expression like we are considering understand the template type parameters from the printout is almost impossible so it is best to visualise them as a tree, e.g,:

For most part the above graph just shows that the assignment, return and expression types are consistent on the precise type of ublas::vector that they deal with. However, one important additional piece of information is that the operation encoded by the binary_expression is just normal addition – this is represented by the scalar_plus type which starts on character 499. So in short the above template type tree tells us that we are have an assignment operator that adds two vectors together!

In the lazy code generation scheme we could simply generate a new version of the assignment operator just described but it is a little simpler to think in terms of free functions. If we follow the call graph from the assignment operator we get to the free function:

void boost::numeric::ublas::vector_assign<boost::numeric::ublas::scalar_assign, boost::numeric::ublas::vector<double, boost::numeric::ublas::unbounded_array<double, std::allocator<double> > >, boost::numeric::ublas::vector_binary<boost::numeric::ublas::vector<double, boost::numeric::ublas::unbounded_array<double, std::allocator<double> > >, boost::numeric::ublas::vector<double, boost::numeric::ublas::unbounded_array<double, std::allocator<double> > >, boost::numeric::ublas::scalar_plus<double, double> > >(boost::numeric::ublas::vector<double, boost::numeric::ublas::unbounded_array<double, std::allocator<double> > >&, boost::numeric::ublas::vector_expression<boost::numeric::ublas::vector_binary<boost::numeric::ublas::vector<double, boost::numeric::ublas::unbounded_array<double, std::allocator<double> > >, boost::numeric::ublas::vector<double, boost::numeric::ublas::unbounded_array<double, std::allocator<double> > >, boost::numeric::ublas::scalar_plus<double, double> > > const&)

which has the types visualisation:

This is the function for which we will later generate alternative code.

It is instructive to look further into the call graph and the actual assembly instructions generated by the compiler as well as the signatures of the functions being called. If all optimisations are turned off, the generated call graph is rather verbose with many functions being called. In fact even the process of actual addition of two numbers is delegated to a separate function, boost::numeric::ublas::scalar_plus<double, double>::apply(double const&, double const&).

Once optimisations are turned on, essentially all of these additional calls are optimised away, and what remains is a loop with a single addsd instruction carrying out the additions and moving the result to the final location. (There is some additional error checking which does not carry a significant error penalty and can be disabled by defining BOOST_UBLAS_NO_EXCEPTIONS). In fact, this code is close to optimal in many situation as the number of operations that can be carried out is limited by the speed of memory access rather than the computation itself.

So can we improve the code generated for the simple array addition? One thing to try is using the a SIMD operation (addpd) rather than the individual addsd. Currently there are several ways in which this could be done:

• Improve the compiler to recognise that in this situation a SIMD instruction could have been used
• Modify the template expression library to generate SIMD instructions
• Hand write the function using the addpd instruction

The first choice is hard because, as I argued above, modifying existing compilers is hard to do and one needs to decide on the hardware to be used at the time of compilation of the main body of the code. The second choice is likewise difficult, and for the same reasons.

Hand-writing a function on the other hand is relatively easy once one figures out the signature to use. Here is an a possible example for the function above, based again on Boost.UBLAS, but with a very minor modification to the vector_binary class that makes members expression1() and expression2() public (we need to access them to get to the underlying data!).

#include <pmmintrin.h>
#include <boost/numeric/ublas/vector.hpp>

namespace boost{ namespace numeric {namespace ublas {

      // This is example of a hand generated assignment!
      template<>
      void vector_assign<boost::numeric::ublas::scalar_assign, 
                         boost::numeric::ublas::vector
                         <double, 
                          boost::numeric::ublas::unbounded_array
                          <double, std::allocator<double> > >, 
                         boost::numeric::ublas::vector_binary
                         <boost::numeric::ublas::vector
                          <double, 
                           boost::numeric::ublas::unbounded_array
                           <double, std::allocator<double> > >, 
                          boost::numeric::ublas::vector
                          <double, 
                           boost::numeric::ublas::unbounded_array
                           <double, std::allocator<double> > >, 
                          boost::numeric::ublas::scalar_plus<double, double> > >
      (boost::numeric::ublas::vector
       <double, 
       boost::numeric::ublas::unbounded_array
       <double, std::allocator<double> > >&a, 
       boost::numeric::ublas::vector_expression
       <boost::numeric::ublas::vector_binary
       <boost::numeric::ublas::vector
       <double, 
       boost::numeric::ublas::unbounded_array
       <double, std::allocator<double> > >, 
       boost::numeric::ublas::vector
       <double, 
       boost::numeric::ublas::unbounded_array
       <double, std::allocator<double> > >, 
       boost::numeric::ublas::scalar_plus<double, double> > > const&b) 
       { 
         typedef double v2df __attribute__ ((mode(V2DF)));
         v2df * dest=(v2df *)&(*a.begin());
         const size_t n=b().expression1().size();
         const v2df *src1=(const v2df *)&(* b().expression1().begin());
         const v2df *src2=(const v2df *)&(* b().expression2().begin());

        if (n%2==0)
        {

          for(size_t i=0; i<n/2; i++)
          {
            dest[i]=__builtin_ia32_addpd(src1[i],src2[i]);
          }
        }
        else
        {
          for(size_t i=0; i<n; ++i)
          {
            dest[i]=src1[i]+src2[i];
          }
        }

      }

    // Close the namespace declaration
    }}}

There are several important points to note with reference to the above function:

• The function signature is long and difficult to write and understand by hand
• We are using a hardware dependent intrinsic call __builtin_ia32_addpd() – this won't work on most platforms
• The hand-coded function is written as a template specialisation

There is a great advantage in using template specialisation: the compiler decides at link time if the specialised or default template implementation is used (in Linux terms, the template generated function is weak). This means that the object generated from the program can be used as is, or, the key functions can be replaced after the compilation of the main body of the program.

In this paper I am just sketching how lazy code generation would work but it is still worth mentioning that the above hand-code function works about 20% faster with arrays of size of around 1000 elements.

The above hand-coded example might improve performance but it has the disadvantage that it is labour intensive to write and maintain. The aim of lazy code generation is to automate the process of writing these specialisations using the following sequence of logical operations:

• Analyse function signatures in object code to extract signatures of expression templates (this is easily done using nm and c++filt tools)
• Analyse expression template signatures to determine the algorithms that they represent
• Identify functions that represent algorithms that the lazy code generator know how to optimise
• Generate the new code for these functions, possibly experimentally benchmarking different implementations on the available hardware
• Compile and link this code with the original object code to produce an optimised executable

While it will no doubt be substantial amount of work to do implement all of these, it is worth noting that there are some tools already available which can do some of the tasks. For example the Theano (http://deeplearning.net/software/theano/) library for Python allows for dynamically building efficient code for expression trees, including support for GPUs.